How to Draw a Circle of Diameter 6 Cm

Selina Concise Mathematics Form vi ICSE Solutions Chapter 29 The Circle

Selina Publishers Concise Mathematics Class six ICSE Solutions Chapter 29 The Circle

ICSE SolutionsSelina ICSE SolutionsML Aggarwal Solutions

APlusTopper.com provides step by step solutions for Selina Curtailed ICSE Solutions for Form 6 Mathematics. You can download the Selina Concise Mathematics ICSE Solutions for Class 6 with Free PDF download choice. Selina Publishers Concise Mathematics for Course six ICSE Solutions all questions are solved and explained past expert mathematic teachers every bit per ICSE board guidelines.

Selina Class 6 Maths ICSE SolutionsPhysicsChemistryBiologyGeographyHistory & Civics

IMPORTANT POINTS

i. A circle is a round enclosed effigy, whose mid-signal is chosen its centre.

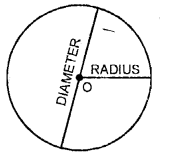
2. The line segment joining the middle to whatsoever point on the circle is called a radius. A centre has space radii and all radii of a circle are equal.
3. A line segment which contains the eye of the circle and whose ends points lie on the circle is called bore of the circle. Diameters of a circle are also equal.
4. Parts of a circumvolve: A circle has three parts (i) Interior (2) Outside and (iii) Circle itself.

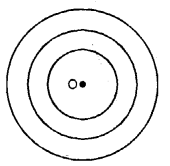
5. Concentric circles: Ii or more circles having the same centre but dissimilar radii are called concentric circles.
half-dozen. Chord of a circle: A line which divides the circle into two parts is called chord of the circle. Diameter is the longest chord of the circle.

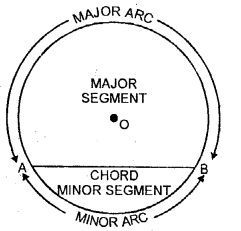
vii. Segment of a circle: When a chord divides the circle into two diff parts, the bigger office is chosen the major segment and smaller part is called the minor segment.
8. Arc of a circumvolve: A role of circumference of a circle is called an arc of the circle. Arc greater than half circle is chosen the major arc and less than half circumvolve is called the small arc.
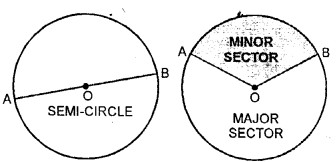
9. Sector of a circle: A bore divides the circle into two equal parts and each function is called a semicircle. Sector greater than a semi-circle is called the major sector and less than semi-circle is called the minor sector of the circle.

The Circumvolve Exercise 29A – Selina Curtailed Mathematics Course 6 ICSE Solutions

Question i.
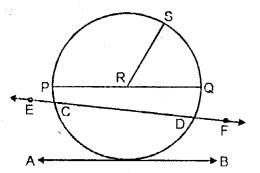
Use the effigy given beneath to fill up in the blanks :
(i) R is the …… of the circle.
(ii) Diameter of a circle is …… .
(iii) Tangent to a circle is … .
(4) EF is a …… of the circumvolve.
(v) …… is a chord of the circle.
(six) Diameter = 2 ten …..
(vii) ……. is a radius of the circle.
(viii) If the length of RS is 5 cm, the length of PQ = ……
(ix) If PQ is 8 cm long, the length of RS =…..
(x) AB is a ….. of the circle

Solution:
(i) heart
(ii) PQ
(3)AB
(iv) secant
(five) CD
(vi) radius
(7) RS
(viii) ten cm
(nine) four cm
(x) tangent.

Question ii.
Describe a circle of radius 4.ii cm. Mark its middle every bit O. Have a point A on the circumference of the circumvolve. Join AO and extend information technology till it meets bespeak B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
Solution:

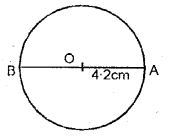
(i) Past measurement AB = 8.4 cm.
(two) ∴ AB is the diameter of the circle.

Question iii.
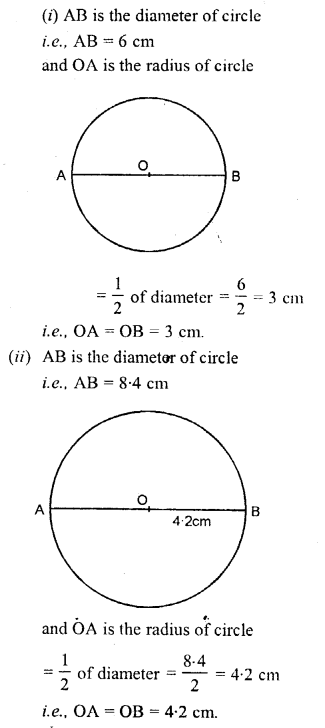
Draw circle with diameter :
(i) vi cm
(ii) eight.4 cm.
In each case, measure the length of the radius of the circumvolve drawn.
Solution:

Question iv.
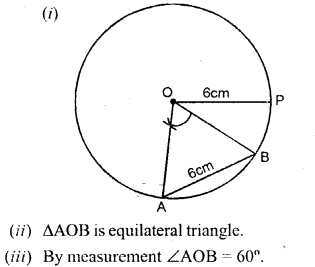
Draw a circle of radius 6 cm. In the circumvolve, draw a chord AB = 6 cm.
(i) If O is the centre of the circle, join OA and OB.
(2) Assign a special name to ∆AOB
(3) Write the mensurate of bending AOB.
Solution:

Question 5.
Describe a circle of radius iv.8 cm and mark its centre as P.
(i) Describe radii PA and PB such that ∠APB = 45°.
(ii) Shade the major sector of the circle
Solution:

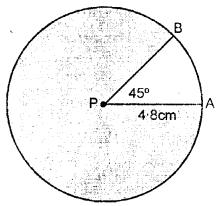
PA is the radius of circle. i.c., PA = 4.8 cm.
(i) ∠APB = 45° in which P is the centre of the circle and PA and PB are radii of circle.
(2) Major sector of circumvolve is shaded in the figure.

Question 6.
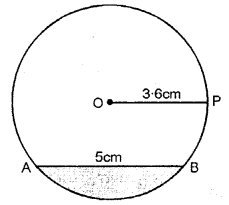
Draw a circumvolve of radius 3.six cm. In the circle, draw a chord AB = five cm. At present shade the minor segment of the circumvolve.
Solution:
Shaded portion of circumvolve is the minor segment of the circle.

Question 7.
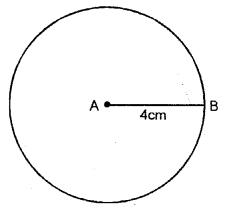
Marker 2 points A and B ,4cm a role, Draw a circle passing through B and with A as a center

Solution:
In the effigy, A is the centre of the circle and AB = four cm [radius of circumvolve]

Question 8.
Depict a line AB = eight.4 cm. Now depict a circle with AB as bore. Mark a indicate C on the circumference of the circumvolve. Measure angle ACB.
Solution:

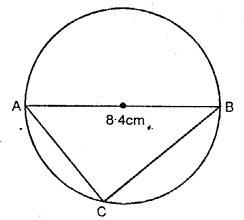
By measurement ∠ACB =90

The Circle Practice 29B – Selina Concise Mathematics Class 6 ICSE Solutions

Question one.
Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and Air-conditioning = 5cm. Construct the circumcircle of the triangle drawn.
Solution:
Steps of Construction :

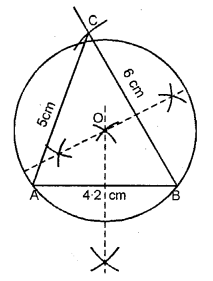
(i) Draw ∆ABC in which AB = 4.2 cm. BC = 6 cm. and Air-conditioning = v cm.
(ii) Depict the perpendicular bisectors of any two sides of the triangle. Let these intersect at O.
(three) Taking O as middle and OA or OB or OC as radius draw a circle.
This circle volition pass through vertices A, B and C.

Question ii.
Construct a triangle PQR with QR = v.5 cm, ∠Q = 60° and bending R = 45°.
Construct the circumcircle cif the triangle PQR.
Solution:
Steps of Construction :

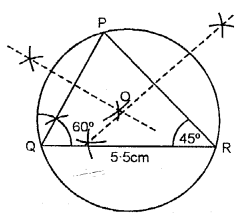
(i) Draw a ∆PQR in which QR = five.5 cm, ∠Q = lx° and ∠R = 45°.
(two) Describe the arc bisector of PQ and PR which intersect at O.
(iii) Taking O as middle and radius OP or OQ or OR depict a circle.
This circumvolve volition pass through vertices P, Q and R.

Question 3.
Construct a triangle ABC with AB = v cm, ∠B = 60° and BC = 6. iv cm.
Draw the incircle of the triangle ABC. Sol. Steps of Structure :
Solution:
Steps of Construction:

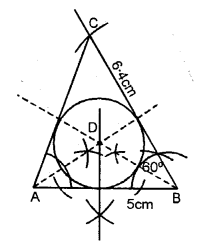
(i) Draw a line AB = 5 cm.
(ii)B equally a centre draw an bending with the help of compass ∠B = lx°. Cut the line with an arc BC = six four cm.
(iii) Bring together Ac.
(iv) Now, from A and B cut the bisector of ∠A and ∠B, which intersect each other at point D.
(five) With D every bit a centre draw an incircle which touches all the three sides of AABC.

Question 4.
Construct a triangle XYZ in which XY = YZ= four.5 cm and ZX = 5.4 cm. Depict the circumcircle of the triangle and measure out its circumradius.
Solution:
Steps of Structure :

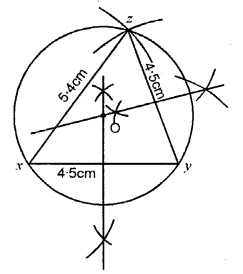
(i) Draw a triangle XYZ in which XY = YZ = 4.five cm and ZX = five.4 cm.
(ii) Draw the bisectors of XZ and YZ which meet at O.
(iii) With O equally center and radius OX or OY or OZ draw a circle.
This circle volition laissez passer through X, Y and Z.

Question five.
Construct a triangle PQR in which, PQ = QR = RP = 5.vii cm. Draw the incircle of the triangle and measure its radius.
Solution:
Steps of Construction :

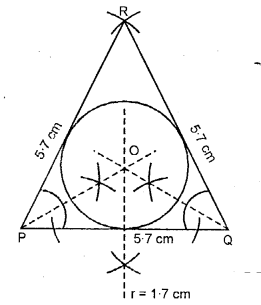
(i) Draw an equilateral ∆ RPQ in which PQ = QR = RP = 5.7 cm each.
(2) From P and Q cut the bisector of ∠P and ∠Q, which intersect each other at signal O.
(iii) With P equally a centre draw an incircle which touches all the three sides of ∆RPQ.

The Circle Revision Exercise – Selina Concise Mathematics Class 6 ICSE Solutions

Question one.
The eye of a circle is at point O and its radius is 8 cm. State the position of a indicate P (point P may lie within the circle, on the circumference of the circle, or outside the circle), when :
(a) OP = 10.six cm
(b) OP = 6.8 cm
(c) OP = eight cm
Solution:
(a) Draw circumvolve each of radius 8 cm. With middle O
In figure (i) depict OP = ten.half-dozen cm

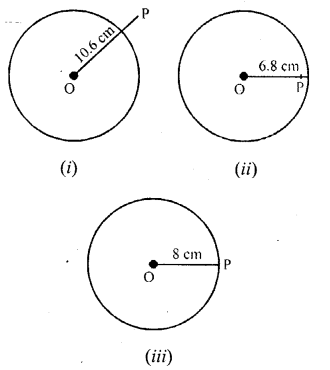
Nosotros see that point P lies outside the circle as OP > radius of the circle
(b) In effigy (ii) OP = six.viii cm. Nosotros see that P lies inside the circumvolve as OP < radius of the circle.
(c) In figure, OP = 8 cm. We see that P lies on the circle as OP = radius of the circumvolve.

Question 2.
The diameter of a circle is 12.6 cm. State, the length of its radius.
Solution:
Diameter of the circumvolve = 12.6 cm
∴Radius = \(\frac { 1 }{ two }\) diameter = \(\frac { 1 }{ ii }\) x 12.6 cm
= 6.3 cm

Question iii.
Can the length of a chord of a circle be greater than its diameter ? Explicate.
Solution:
No, the length of chord cannot be greater than the bore of the cirlce as the bore of a circle is the greatest chord of that circle.

Question iv.
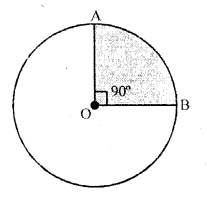
Draw a circle of bore seven cm. Draw two radii of this circle such that the angle betwixt these radii is xc°. Shade the small-scale sector obtained. Write a special name for this sector.
Solution:
Describe a circle with diameter = 7 cm
OA and OB are the radii of the circle such that ∠AOB = 90°
Now shade the minor sector AOB This is the quadrant of the circle

Question v.
State, which of following statements are true and which are imitation :
(i) If the terminate points A and B of the line segment lie on the circumference of a circumvolve, AB is a diameter.
(ii) The longest chord of a circle is its bore.
(iii) Every diameter bisects a circle and each part of the circle and then obtained is a semi-circle.
(iv) The diameters of a circle always laissez passer through the same indicate in the circle.
Solution:
(i) False, as AB may exist bore or may non be, information technology tin can be chord.
(ii) Truthful, diameter of a circumvolve is the longest chord.
(3) True.
(iv) True, all the diameter of a circle pass through the aforementioned point i.e., centre, of the circle.

barberroake1989.blogspot.com

Source: https://www.aplustopper.com/selina-concise-mathematics-class-6-icse-solutions-the-circle/

Share this post